Les maths de GeoGuessr

Coordonnées

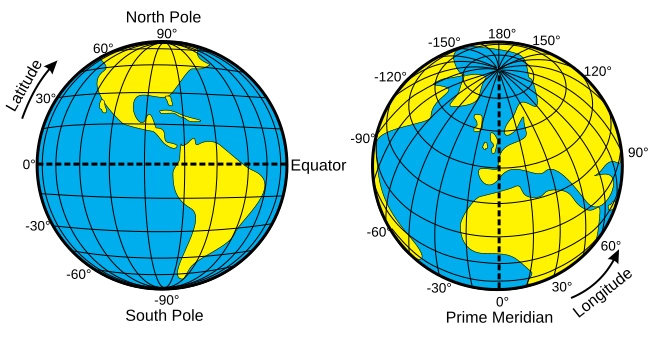
La terre est à peu près ronde (si si) et elle est considérée comme étant une sphère parfaite de 6371 km de rayon dans GeoGuessr.
Elle tourne autour d'un axe de rotatation sur lesquels sont placés le pôle Nord et le pôle Sud.
Les positions sur la terre sont définies avec leurs positions sur deux cercles.

Le cercle situé entre ces deux pôles est appelé l'équateur.
Les cercles parallèles à l'équateur sont appelés ... parallèles.
Ils sont mesurés de -90° (Le pôle sud) à +90° (Le pôle nord).
Cette mesure est appelée latitude.

Les cercles perpendiculaires aux parallèles sont les méridiens, ils passent tous par les pôles.
Il n'y a pas de méridien de référence naturel mais pour des raisons historiques, le méridien 0 passe près de l'observatoire de Greenwich.
Ils sont mesurés de -180° à +180°.
Cette mesure est appelée longitude.

Mercator

Il n'est pas possible de représenter sur une carte plate toutes les caractéristiques (formes, distances, surfaces ...) de la géographie réelle sur le globe.
La projection la plus couramment utilisée, dont dans GeoGuessr, est la projection de Mercator qui a l'avantage de conserver les formes au niveau local, ce qui fait que ce qu'on voit autour de soit est conforme à ce qu'on voit sur la carte, par contre les représentation des distances et surfaces sont très différentes entre des points de latitudes différentes.

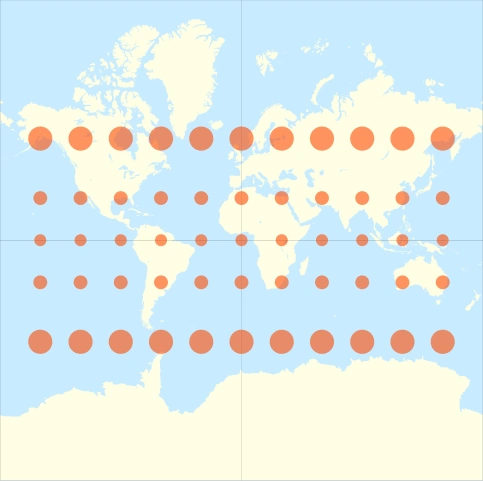
C'est grâce à la projection de Mercator que la technique consistant à identifier une route en regardant le sol boussole vers le nord et en comparant l'orientation par rapport aux routes sur la carte marche.

Par exemple, voici à quoi ressemble Oslo avec la projection de Mercator et avec la projection équirectangulaire :

⚠️ Maths
Les méridiens font tous la même longueur, donc pour un déplacement d'un degré le long d'un méridien, on a une distance de 6371000 * π / 180 = 11195 m.
La longueur des parallèles diminue à mesure qu'on s'éloigne de l'équateur en fonction du cosinus de la latitude, donc pour un déplacement d'un degré le long d'un parallèle se calcule donc avec la formule suivante, on a une distance de cos(lat) * 6371000 * π / 180 m.
C'est pourquoi avec la projection équirectangulaire, à Oslo, les distances horizontales sont divisées par deux (cos(60°) = 0.5).
Pour la projection de Mercator, il faut qu'à une certaine coordonnée, un déplacement d'un pixel verticalement ou horizontalement corresponde à la même distance.
Le rapport entre la longitude et l'abcisse est contraint par la forme cylindrique de la projection, pour simplifier le calcul suivant, on peut se projeter entre - π et π, on a donc x = lng * π / 180.
En un point donné, dx / dlng = π / 180, donc dy / dlat = π / 180 / cos(lat) et avec un peu de magie on trouve y = ln(tan(lat * π / 180 / 2 + π / 4)).
Si on fait la projection jusqu'aux pôles, la carte devrait être infiniement grande et serait extrêmement déformée, les cartes se limitent en général à un format carré, la latitude maximle vaut donc (atan(exp(π)) - π / 4) * 2 * 180 / π = 85.0511°.
Cette limite est au délà des dernières terres dans l'hémisphère nord et au sud de la quasi totalité des bases en antarctique, à l'exception de la base Amundsen-Scott située au pôle sud.

Niveau de Zoom

Pour savoir quoi télécharger et afficher à l'écran, en plus des coordonnées, les service de cartographie en ligne utilisent un niveau de zoom standardisé.
Le niveau de zoom 0 correspond à une image de 256 pixels de côté allant de -180° à 180° de longitude et de -85.0511° à 85.0511° de latitude.

Voici la tuile correspondante dans Open Street Map :

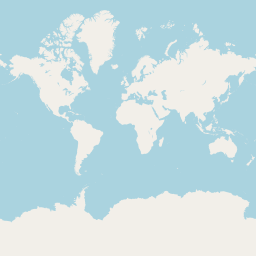
À chaque fois que le niveau de zoom est doublé, on divise l'image précédente en quatre sous carrés, chacun avec une image de 256 pixels de côté correspondante.
Différentes informations (frontières, noms des pays, villes ...) sont accessibles à différents niveaux de zoom selon les services.

Les trois liens suivants pointent vers les mêmes coordonnées avec le même niveau de zoom sur différents services de cartographie (les cartes ne sont pas exactement centrées au même endroit car ça dépend aussi de l'interface du site) :
https://www.google.fr/maps/@43.6044,1.4437,15z
https://www.openstreetmap.org/#map=15/43.6044/1.4437
https://wego.here.com/?x=ep&map=43.6044,1.4437,15,normal

Dans GeoGuessr, le niveau de zoom minimal est de 1.

Carte interactive

La carte suivante montre le niveau de zoom actuel de la carte, ainsi que des informations au niveau du curseur

Distance

GeoGuessr calcule les distances en utilisant la formule de Haversine et en prenant un rayon terrestre de 6371 km.
La distance maximale est donc de 6371 km * π ≈ 20015 km.

Score

Pour chaque carte, GeoGuessr calcule des latitudes et longitudes limites entourant l'ensemble des points pour faire un rectangle.
Pour les latitudes, c'est simple, c'est toujours les latitudes les plus au sud et au nord.
Pour les longitudes, c'est un poil particulier, c'est les longitudes les plus extrèmes entre -180 et +180.

Par exemple, sur la carte suivante : Démo maths
GeoGuessr fait un rectangle entre les lattitudes 38.689669° (correspondant au point à Lisbonne) et 60.176403° (correspondant au point à Helsinki) et les longitudes -9.177197° (correspondant au point à Lisbonne) et 37.624274° (correspondant au point à Moscou).

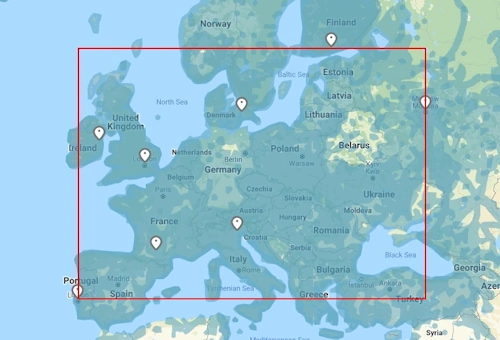
Après, à partir de ces valeurs, GeoGuessr calcule la diagonale du rectangle (ou plutôt le distance la plus courte entre ses deux extrémités, la nuance est illustrée plus bas) que l'on appelera D par la suite.
Par exemple, toujours pour cette carte : calcul
On trouve D ≈ 4014 km.

On peut trouver une distance similaire en prenant la diagonale sur Google Maps, les points ne correspondant pas tout à fait.

Cas particulier : Pour la carte Famous Places, la distance prise en compte vaut 1/10 de cette diagonale.

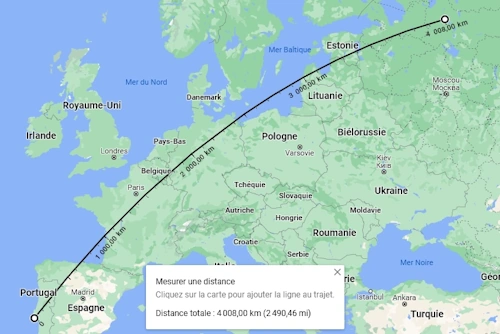
Ensuite, quand on joue, GeoGuessr calcule, avec la même formule, la distance entre le point deviné et le bon point, que l'on appelera d.
Le score sur 5000 est alors calculé avec la formule suivante :
S = 5000 * exp(- 10 * d / D)
Par exemple, toujours pour la carte de démo, voici le score en fonction de la distance sur les 1000 premiers kilomètres : calcul

À partir de cette formule, on peut par exemple déterminer la distance maximale pour faire 5000 sur cette carte : calcul
Il faut donc faire moins de 40.14 m sur la carte de démo pour faire 5000.

Et voici la distance à faire pour plusieurs scores de référence:

De manière générale, le seuil pour faire 5000 vaut environ 1 / 100000 de la diagonale : calcul
Ce seuil augmente d'environ 2 / 100000 par point pour les quelques premières centaines de points : calcul

Il y a cependant une exception, Quelque soit la taille de la carte, une distance de moins de 25 m fait toujours 5000.
Du coup, sur les cartes très petites, comme Toulouse, on passe de 5000 à 4931 d'un coup après les 25 m.

Pour avoir exactement le même barème qu'une carte existante, il faut donc mettre deux points à des extrémités opposées du rectangle, il n'y a pas besoin que ces points existent réellement, on peut les importer en csv.
On se retrouver alors avec une carte de 7 points dont 5 qui nous intéressent et, à chaque génération, on a 5/7*4/6*3/5*2/4*1/3 = 1/21 chance de tomber sur une seed avec les 5 points qui nous intéressent.

Vous pouvez accèder aux bornes et au barème des cartes de GeoGuessr avec la fonction "Informations sur la carte" de GeoGuessr Tweaks.

Il était une fois dans l'ouest

pour les cartes type France ou Europe, la façon de calculer la diagonale ne pose pas de problème, pour une carte contenant des points dans le Pacifique, ça peut poser problème.

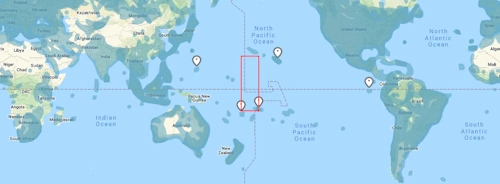
Par exemple sur la carte suivante, on pourrait s'attendre à ce que GeoGuessr prenne ce rectangle là :

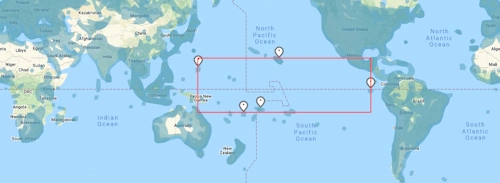
Mais en réalité il va prendre en compte ce rectangle là :

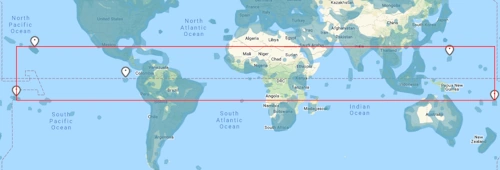
La distance la plus courte entre les deux extrémités sera alors celle de ce rectangle là et l'échelle des scores sera très compliquée :

Interro surprise !

Sur une carte dont les bornes sont définies par un point au pont du 25 avril à Lisbonne, un point au pont du Bolshoy à Moscou et un point au pont Pitkäsilta à Helsinki, si au lieu d'un point sur le Pont Neuf à Toulouse, je me place au pont de Westminster à Londres, quel est mon score ?

Probabilités de générations de seeds

⚠️ Tous les calculs qui suivent supposent que chaque point d'une carte à la même probabilité de tomber, ce qui n'est peut-être pas tout à fait le cas !

Probabilité d'avoir certains points d'une carte comprenant plus de 5 points

Si on met une ou des bornes, pour changer le courbe des scores ou le centrage de la carte par défaut, les challenges générés risquent de contenir une de ces bornes.
Si on met une seule borne, au premier round on a 5 points acceptables parmis les 6 points de la carte, au deuxième round on a 4 points acceptables parmis les 5 points restants, et ainsi de suite jusqu'au dernier round où on a 1 point valables parmis les 2 restants. La probabilité qu'une seed contienne les 5 points qui nous intéresse est donc de 5/6*4/5*3/4*2/3*1/2 = 1/6.
De la même manière, si on a deux points bornes, on a 5/7*4/6*3/5*2/4*1/3 = 1/21 chance de tomber sur une seed avec les 5 points qui nous intéressent.

Probabilité d'avoir certains points à des positions prédéfinies

Une fois qu'on a 5 points, il y a 5 possibilités pour le premier, 4 possibilités pour le deuxième, 3 pour le troisième, 2 pour quatrième et une seule pour le dernier, ce qui fait 5*4*3*2*1 = 120 ordres possibles. Selon le mode de jeu, on peut vouloir imposer les positions de certains points.
Si on veut imposer les 5 points dans un ordre précis, on a 1/120 chances d'avoir la bonne seed.
Si on veut juste imposer le dernier point, on a 1/5 chances de l'avoir.

Ces probabiltés sont à multiplier aux probabilités d'avoir les 5 points, par exemple pour imposer le dernier point d'une carte avec une borne, on aura une probabilité de 1/5*1/6 = 1/30 d'avoir une bonne seed.

Probabilité que des seeds correspondent entre elles

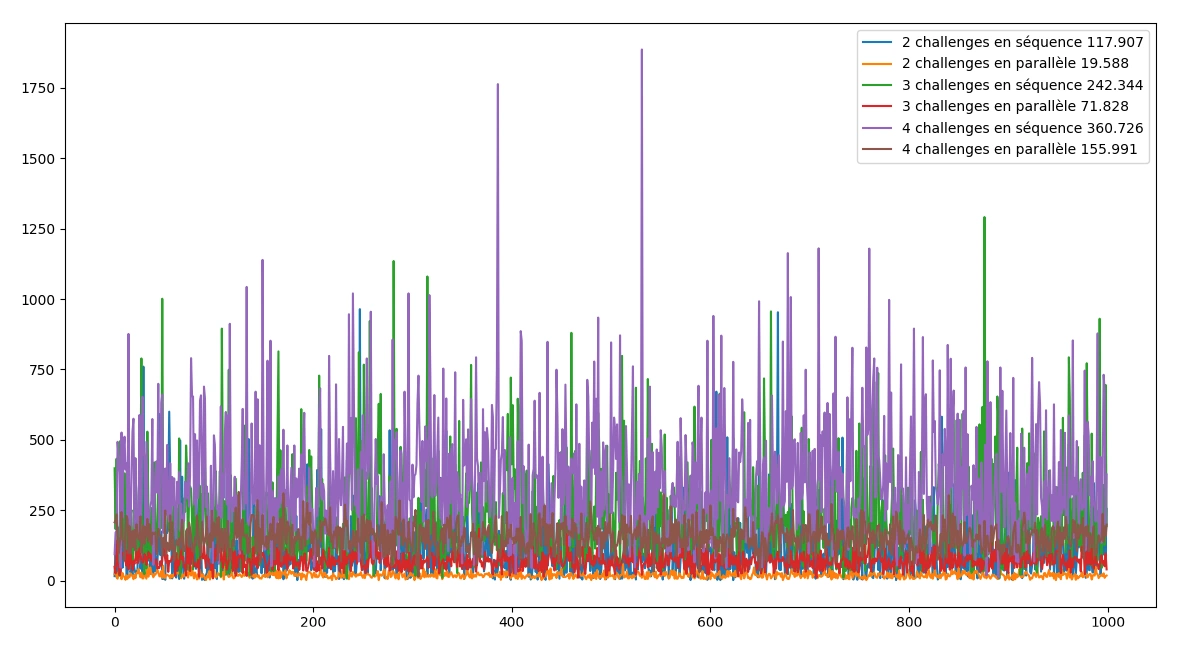
Pour certains modes de jeux, on a besoin d'avoir plusieurs challenges sur plusieurs seeds dont les points correspondent entre eux.

La façon la plus basique consiste à générer la seed de la première carte, puis à générer des seeds sur les autres cartes en espérant tomber sur le même ordre que la seed de la première carte. Ce qui a une 1/120 chance de se produire à chaque fois.

Une technique plus efficace, trouvée par Qubillou, consiste à générer des seeds en parallèle sur chaque carte jusqu'à en trouver une commune. Ainsi, la probabilité augmente au fil du temps car les seeds sont comparées à de plus en plus d'autres seeds à chaque fois.

Voici le résultat de la simulation de 1000 génération de seeds les deux méthodes, avec le nombre moyen d'essais pour y arriver.