The maths of GeoGuessr

Version française

Coordinates

Earth is mostly round (yes it is!) and is considered as a perfect sphere of 6371 km of radius in GeoGuessr.
It rotates around an axis of totation on which are places the North pole and the South pole.
Positions on earth are defined with their positions on two circles.

The circle between the two poles is called the equator.
The circles parallel to the equator are called... parallels.
The are measured from -90° (the South pole) to +90° (the North pole).
This measure is called latitude.

Circles perpendicular to the parallels are called meridians, the all go through the poles.
There is no natural reference meridian, but for historical reasons, meridian 0 is next to Greenwich observatory.
They are measured from -180° to +180°.
This measure is called longitude.

Mercator

It's not possible to represent on a map every characteristics (shapes, distances, areas...) of the real geography on the globe
The most commonly used projection, including in GeoGuessr, is the Mercator projection, which has the advantage of preserving the shapes at close range, which means that what we see around us is consistent whith what we see on the map, but the distances and areas are very different between locations at different latitudes.

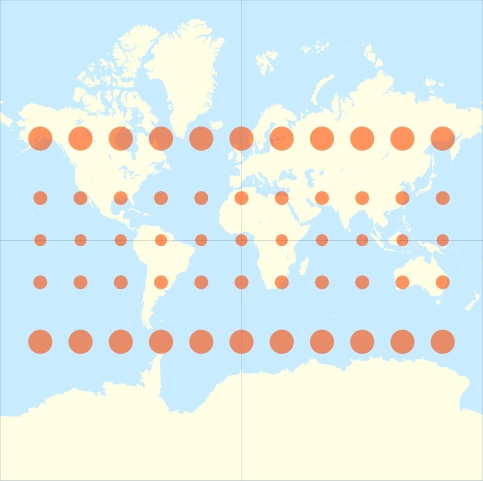
It's thanks to the Mercator projection that we can look at the road with the compass to the north and compare its orientation with the roads on the map.

For example, here is what Oslo looks like with the Mercator projection and with the Equirectangular projection:

⚠️ Maths
Meridians are all the same length, so for a one degree shift along a meridian, we have a distance of 6371000 * π / 180 = 111195 m.
The length of the parallels decreases as we move away from the equator depending on the cosine of the latitude, so for a one degree shift along a parallel, we have a distance of cos(lat) * 6371000 * π / 180 m.
This is why with the Equirectangular projection, in Oslo, horizontal distances are divided by two (cos(60°) = 0.5).
For Mercator projection, for any coordinates, a shift of one pixel verticaly or horizontaly correspond to the same distance.
The relationship between longitude and abscissa is constrained by the cylindrical shape of the projection, so x = lng * π / 180.
For a given point, dx / dlng = π / 180, so dy / dlat = π / 180 / cos(lat) and with a bit of magic we find y = ln(tan(lat * π / 180 / 2 + π / 4)).
If we us this projection up until the poles, the map would have to be infinitely large and extremely distorted. Maps are generally limited to a square shape, so the maximum latitude is (atan(exp(π)) - π / 4) * 2 * 180 / π = 85.0511°.
This limit is beyond any landmass in the northen hemisphere and south of almost every base in Antartica, except for Amundsen-Scott base which is located at the South Pole. On Google Street View, this base is represented at the wrong coordinates to be visible on the map.

Zoom level

To know what image to download and display, in addition to the coordinates, map services use a standardized zoom level.
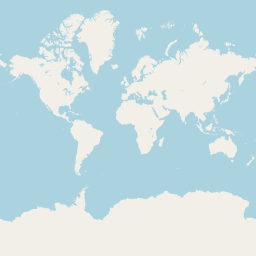
Zoom level 0 corresponds to an image of 256 pixels going from -180° to 180° of longitude and from -85.0511° to 85.0511° of latitude.

Here is the corresponding tile in Open Street Map :

Each time the zoom level is doubled, the previous image is divised into four sub squares, each with a 256 pixels corresponding image.
Different information (borders, country names, citiy names...) is accessible at different zoom levels depending on the services.

Here are the same coordinates at the same zoom level on some services:
https://www.google.com/maps/@43.6044,1.4437,15z
https://www.openstreetmap.org/#map=15/43.6044/1.4437
https://wego.here.com/?x=ep&map=43.6044,1.4437,15,normal

In GeoGuessr, the initial zoom level is 1.

Interactive map

The following map shows the current zoom level of the map, and additional information at the cursor location.

Distance

GeoGuessr computes distances using Haversine formula with an earth radius of 6371 km.
So the maximum distance is 6371 km * π ≈ 20015 km.

Score

For each map, GeoGuessr computes the latitudes and longitudes of the bounds of the rectangle surrounding all the locations.
For latitudes, it's simple, it'w always the southernmost and the northernmost latitudes.
For the longitudes, it's a bit different, it's the most extreme longitudes between -180 and +180.

For example, on this map: Démo maths
GeoGuessr makes a rectangle between the latitudes 38.689669° (Lisbonne) and 60.176403° (Helsinki) and the longitudes -9.177197° (Lisbonne) and 37.624274° (Moscou).

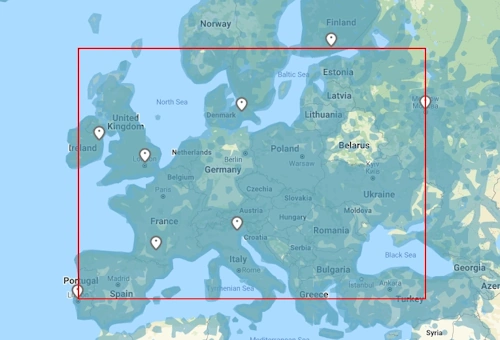
Then, from these values, GeoGuessr computes the length of the diagonal of the rectangle (or rather the shortest distance between its two ends, the naunce is illustrated below), which we will call D hereafter.
For example, on this map: calculus
We found D ≈ 4014 km.

We can find a similar distance taking the approximate diagonal on Google Maps.

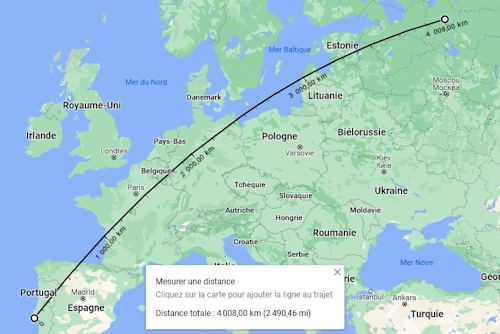
Then, when we play, GeoGuessr computes, with the same formula, the distance between the guessed location and the good location, that we will call d.
The score on 5000 is then computed with the following formula:
S = 5000 * exp(- 10 * d / D)
For example, always on the same demo map, here is the score in relation to the distance for the first 1000 kilometers: calculus

From this formula, we can get the maximal distance to do 5000 on this map: calculus
So we need to do less than 40.14 m on this map to score 5000.

And here is the distance for some scores:

Generally, the threshold to score 5000 is about 1 / 100000 of the diagonal: calculus
This threshold is increased of about 2 / 100000 per point for the first few hundered points: calculus

There is an exception, whatever the size of the map, a distance of less than 25 m will always score 5000.
So, for very small maps, like city maps, you will drop a few hundered points just after the 25 m.

To have exactly the same scale as an existing map, you need to place the same two locations at the opposite end of the rectangle, there is no need for these locations to actyally exist.
We then end up with a map of 7 locations, 5 of us being interresting for us, and at each generation, we have 5/7*4/6*3/5*2/4*1/3 = 1/21 chance of finding a seed with the 5 locations we want.

Special case: It's now possible to manually adjust this distance, in order to refine the 5k radius.

You can access the bounds and the scale of the maps in GeoGuessr with the tool "Map information" of GeoGuessr Tweaks.

Once upon a time in the west

For a map like France or Europe, the way to compute the diagonal is not a problem, but it can be for a map with locations in the Pacific.

For example, on the following map, we could excpect GeoGuessr to take this rectangle:

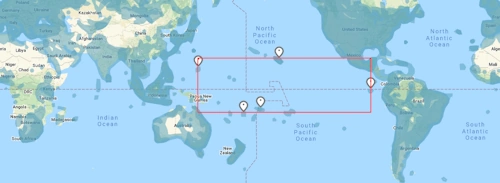
But instead, it will take this rectangle:

So the shortest distance between its extremity will be this one and the scaling will be very difficult:

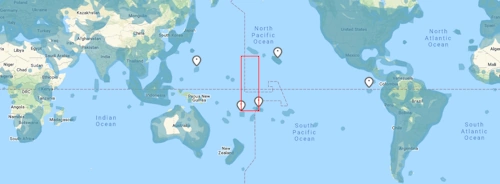
Seeds generation probabilities

⚠️ This section is heavily obsolete since GeoGuessr allows us to choose the orders of locations in a challenge (October first 2025 update)
⚠️ Every calculation is made assuming that every location of a map has the same probability to be picked, which may not be exactly the case!

Probability to have some locations of a map of more than 5 locations

If we had one or two bounds to a map, to change the scoring or the default map centering, generated challenges may contain one of these.
If we add a single boundary, for the first rounds, we have 5 acceptables locations out of 6, then at the second 4 out of 5, and so on, until the last round for which we have one acceptable location out of the 2 left. Therefore, the probability that a seed contains the 5 locations that we want is 5/6*4/5*3/4*2/3*1/2 = 1/6.
The same way, if we have two bounds, we have 5/7*4/6*3/5*2/4*1/3 = 1/21 probability to get a seed with the 5 locations that we want.

Probability to have some locations at some predefined rounds

Once we have 5 locations, there is 5 possibilities for the first round, 4 for the second round, 3 for the third round, 2 for the fourth round and one for the last round, which makes 5*4*3*2*1 = 120 possible orders. Depending of the gamemode, we may want to fix the round number of some locations.
If we want to fix the 5 locations in a precise order, we have 1/120 probability to get the good seed.
If we just want to fix the last round, on have 1/5 probability to get it.

These probabilities have to be multiplied by the probability of having 5 locations, for example, to fix the last location of a map with one bound, we have a probability of 1/5*1/6 = 1/30 to get a good seed.

Probability that several seeds have the same order

For some gamemodes, we need to have several challenges over several seeds which locations are in the same order.

The basic way to do it is to generate the seed of the first map, then to generate the seeds of the other maps hoping to have the same order as the seed from the first map. Which has a probability of 1/120 every time.

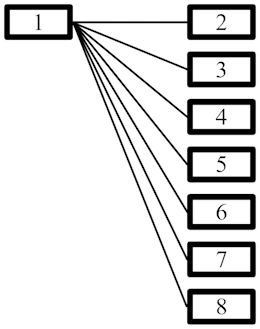
A more efficient technique, found by Qubillou, is to generate the seeds in parallel on each map until we find the same order. So, the probability increase every time because the seeds are compared to more and more seeds every time.

Here is the resul of the simulation of 1000 generations of seeds with the two methods, with the mean number of tries to get it.